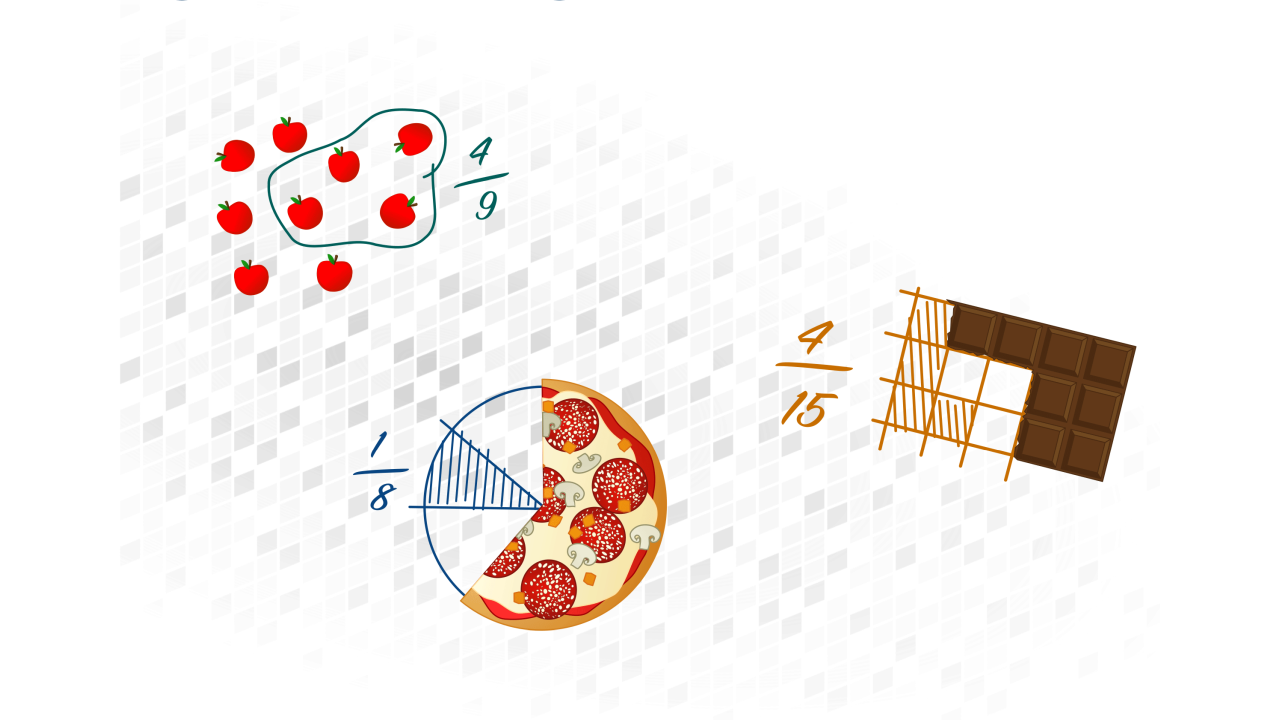Tom und Uli vergleichen Brüche: Welcher Bruch ist größer? \frac{5}{8} oder \frac{5}{10}?
Tom sagt: “Der Bruch \frac{5}{10} ist größer als der Bruch \frac{5}{8}, weil der Zähler größer ist”.
Uli ist anderer Meinung: “Wenn ein Kuchen in acht Stücke geteilt wird, alle sind gleichgroß, dann ist ein Stück größer als würde der Kuchen in zehn gleichgroße Stücke geteilt werden …”
Die zunehmende Heterogenität im Klassenraum schafft manche Vorteile, birgt aber auch Herausforderungen für guten Mathematikunterricht. Wie lassen sich Schülerinnen und Schülern unterschiedlicher Leistungsniveaus in einer Klasse adäquat fördern? Gerade in schwierigen und zentralen Teilbereichen der mathematischen Grundbildung wie der Bruchrechnung? Das erfordert eine hohe fachdidaktische Expertise. Digitale Werkzeuge können hier zunehmend unterstützen: Gut gestaltete digitale Lernumgebungen stellen Schülerinnen und Schülern individuell angepasste Lerngelegenheiten zur Verfügung, die sich an ihren spezifischen Bedürfnissen orientieren.
Wie kann man Bruchzahlverstehen mithilfe digitaler Medien fördern?
Sicherlich haben Sie selbst schon einige Erfahrungen damit gemacht, welche Herausforderungen es bei der Einführung von Bruchrechnung geben kann. Vielleicht haben Sie überlegt,
- warum Schülerinnen und Schüler häufig Verständnisschwierigkeiten bei Bruchzahlen haben,
- wie Sie digitale Lernumgebungen mit Bildern, Animationen, Texten und Videos lernförderlich gestalten,
- welche Potenziale digitale Lernsoftware beispielsweise für die Differenzierung hat.
Wir möchten Ihnen hier einige Erkenntnisse aus Sicht der fachdidaktischen und lernpsychologischen Forschung vorstellen, zur Entwicklung des Bruchzahlbegriffs, zur Gestaltung von Lernmaterialien und zu Potenzialen digitaler Medien. Für Sie sind Materialien für den Einsatz im Unterricht (forschungsbasiertes Schulbuch zum Bruchrechnen) und in Fortbildungen für Lehrkräfte (Arbeitsblätter zu den hier vorgestellten Inhalten) kostenlos verfügbar. Falls Sie sich tiefer mit diesem Thema beschäftigen möchten, geben wir Ihnen Anregungen zum Ausprobieren des Materials, zur Umsetzung in Ihrer Praxis und die Möglichkeit, Ihr eigenes Wissen mit einem Selbsttest zu überprüfen.
Für eilige Leser halten wir eine Zusammenfassung bereit.
Entwicklung des Bruchzahlbegriffs
Bei der Zahlbereichserweiterung von natürlichen Zahlen zu Bruchzahlen verändert sich das konzeptuelle Verständnis dessen, was man unter Zahlen versteht. Diese Unterschiede, die stets mit einer notwendigen Veränderung des Verständnisses von Zahlen einhergehen, lassen sich grob in vier Teilbereiche einordnen (z.B. Obersteiner, Van Hoof, Verschaffel & Van Dooren, 2015):
- Während natürliche Zahlen eine eindeutige symbolische Darstellung haben, können wertgleiche Brüche durch verschiedene Symbole repräsentiert sein (z.B. \frac{1}{2}=\frac{2}{4}). Sogar natürliche Zahlen verlieren im Zahlbereich der rationalen Zahlen ihre eindeutige Darstellung (z. B. 2=\frac{4}{2}=\frac{6}{3}).
- Das von den natürlichen Zahlen wohlbekannte Konzept des Nachfolgers existiert im Kontext von Bruchzahlen nicht mehr, denn die rationalen Zahlen bilden eine dichte Teilmenge der reellen Zahlen. Jedoch kann an dieser Stelle in Klasse 6 kein fachlich einwandfreies Konzept von Dichte vermittelt werden.
- Die Frage nach der größeren von zwei vorgegebenen natürlichen Zahlen ist weitgehend einfach unter Rückgriff auf die Ziffernschreibweise zu beantworten. Das Konzept der Größe von Bruchzahlen unterscheidet sich hiervon grundlegend. So ist etwa \frac{8}{9}<\frac{7}{6}, obwohl 8 > 7 und 9 > 6. Dieser Schritt bereitet Schülerinnen und Schüler zum Teil erhebliche Schwierigkeiten, wenn sie an Konzepten natürlicher Zahlen festhalten. So sind Schülerantworten keine Seltenheit, in der \frac{8}{9} fälschlicherweise als der größere Bruch interpretiert wird, „weil der Zähler größer ist“.
- Auch die Interpretation grundlegender Rechenoperationen verändert sich bei der Zahlbereichserweiterung. Gängige Grundvorstellungen, etwa der Multiplikation als „wiederholtes Addieren“, verlieren oder verändern ihre Bedeutung. Auch, dass „Multiplizieren vergrößert“, verliert seine allgemeine Gültigkeit. So kann z. B. die Rechnung \frac{1}{2} \cdot 4 weder als wiederholte Addition von 4 erklärt werden, noch ist das Ergebnis 2 größer als der zweite Faktor 4.
Man geht davon aus, dass Schülerinnen und Schüler erhebliche Probleme bei der Entwicklung einer tragfähigen Vorstellung von Bruchzahlen haben, wenn sie an Konzepten natürlicher Zahlen festhalten.
Es hat sich gezeigt, dass eine Fokussierung im Unterricht auf arithmetische Operationen sowie den Umgang mit der formal-symbolischen Schreibweise von Brüchen alleine meist nicht gewinnbringend ist. Vielmehr wird angenommen, dass gerade im Anfangsunterricht der Bruchrechnung die Verwendung bildhafter Darstellungen sowie der durch die Lehrkraft angeleitete und beständige Wechsel zwischen unterschiedlichen Repräsentationen von Brüchen sehr praktikable fachdidaktische Herangehensweisen darstellen. Gerade in diesem Zusammenhang wird auch digitalen Unterrichtsmedien bereits seit geraumer Zeit ein großes Potential beigemessen (z. B. Lesh, Post & Behr, 1987).
Der Wechsel zwischen Repräsentationen kann zum Beispiel bei der Einführung von Brüchen als Teil vom Ganzen schrittweise eingeführt werden. Das operative Vorgehen bei der Bildung eines „Teils \frac{a}{b} vom Ganzen“ erfolgt für ikonische und symbolische Darstellung gleich: Zunächst wird das Ganze identifiziert. Anschließend wird es in b gleich große Teile zerlegt (en.: partitioning). Von diesen Teilen werden a Stücke genommen. Das Resultat ergibt den gesuchten Bruchteil (z.B. Behr, Lesh, Post & Silver, 1983). Diesem Vorgehen liegt eine operative Vorgehensweise zu Grunde. Es ist dabei unabhängig davon, ob das Ganze ikonisch kontinuierlich, diskret, oder formal symbolisch angegeben wird (Baturo & Cooper, 1999).
Öffnen Sie das digitale Schulbuch auf Seite 18. In der interaktiven Aufgabe 17 sollen Teile vom Ganzen nach dem oben erläuterten Schema berechnet werden. Wie kann eine vorhergehende Bearbeitung ikonischer Aufgaben den Lernprozess in dieser interaktiven Aufgabe unterstützen? In welcher Form erfolgt diese Unterstützung in der interaktiven Aufgabe?
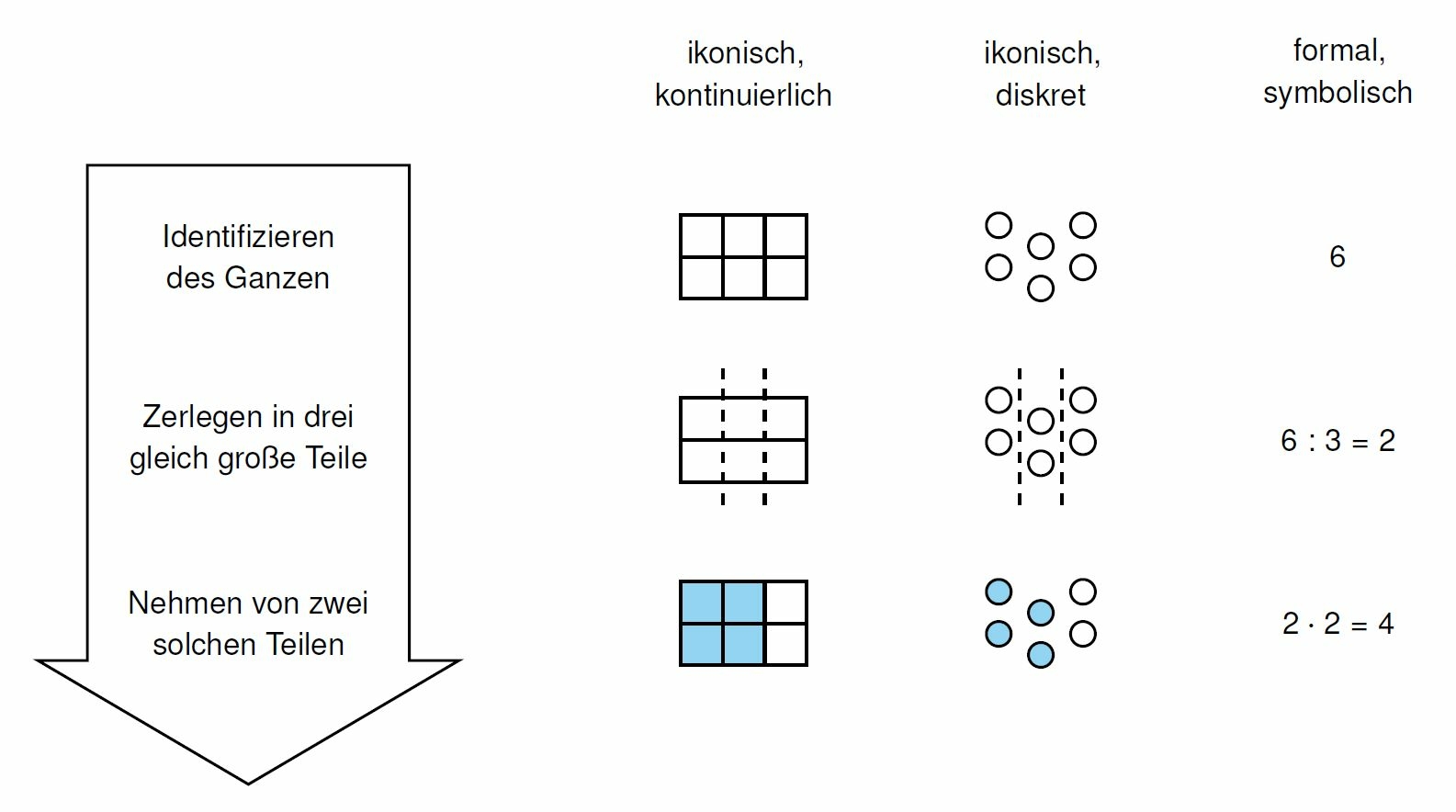
Lösung
Das operative Vorgehen kann für Schülerinnen und Schüler zu Beginn der Bruchrechnung eine erhebliche Herausforderung darstellen. Eine Einführung zunächst anhand konkreter Handlungen und ikonischen Darstellungen kann hier zu einer kognitiven Entlastung führen und den Lernprozess von Kindern geeignet unterstützen (Bruner, 1977). Das in der interaktiven Aufgabe implementierte System abgestufter Lösungshilfen greift auf die Anschauungen der konkreten Handlungen „Zerlegen“ und „Vervielfachen“ zurück. Nachdem das operative Vorgehen verstanden ist, können weitere Darstellungsformen eingeführt werden, an denen Teile vom Ganzen berechnet werden; auch symbolische. Der Wechsel zwischen Repräsentationen kann die Anwendung des operativen Vorgehens flexibilisieren und so das Verständnis vertiefen.
Gestaltung von Lernmaterial
Das Interpretieren bildhafter Darstellungen und der Wechsel zwischen verschiedenen Darstellungsformen wie Pizzen und Schokoladentafeln fällt Schülerinnen und Schülern oft schwer. Sie müssen gleichzeitig mehrere Aufgaben bewältigen: den eigentlichen Lerngegenstand verstehen, die Darstellungsform interpretieren und Informationen aus den verschiedenen Darstellungsformen integrieren. Die Theorie der kognitiven Belastung (1) sowie die kognitive Theorie des multimedialen Lernens (2) können erklären, warum dies vielen Lernenden nicht leicht fällt.
Theorie der kognitiven Belastung
Die Grundannahme der Theorie der kognitiven Belastung ist eine beschränkte Kapazität des menschlichen Arbeitsgedächtnisses. Dies bedeutet, dass die Anzahl von Informationen beschränkt ist, die Lernende gleichzeitig verarbeiten können. Wieviele Informationen das sind, unterscheidet sich zwischen Lernenden und hängt zum Beispiel von ihrem Vorwissen ab.
Man geht davon aus, dass sich die für das Erlernen einer Fähigkeit benötigte kognitive Belastung aus drei Komponenten zusammensetzt:
- Intrinsische kognitive Belastung: Die dem Material selbst inhärente Schwierigkeit, die durch Vorwissen individuell unterschiedlich für jeden Schüler und jede Schülerin ausfallen kann.
- Irrelevante kognitive Belastung: Die kognitive Belastung, die durch die Art und Weise, wie das Material präsentiert wird, hervorgerufen wird. Sie unterstützt keine Lernprozesse.
- Lernbezogene kognitive Belastung: Elemente, die die Informationsverarbeitung unterstützen können und zur Entwicklung von Wissensstrukturen (sogenannte Schemata) beitragen können.
Es wird angenommen, dass Lernprozesse nur gelingen können, wenn die gesamte kognitive Belastung die Kapazität des Arbeitsgedächtnisses nicht überschreitet.
Kognitive Theorie des multimedialen Lernens
Die kognitive Theorie des multimedialen Lernens gründet neben einer beschränkten Kapazität des Arbeitsgedächtnisses auf weiteren Annahmen: Zum einen geht man davon aus, dass Menschen einerseits auditiv und visuell dargebotene Informationen in jeweils unterschiedlichen kognitiven Strukturen verarbeiten. Weiter wird angenommen, dass auch in Texten und Bildern dargestellte Informationen in wieder unterschiedlichen kognitiven Strukturen verarbeiten. Darüber hinaus wird Lernen als ein aktiver Prozess verstanden, bei dem Wissen durch gezielte Auseinandersetzung mit einem Lerngegenstand in bestehende Wissensstrukturen eingegliedert werden muss.
Die kognitive Theorie des multimedialen Lernens empfiehlt Prinzipien, wie Darstellungen so gestaltet werden können, damit sie möglichst lernförderlich sind. Eines davon ist das Kontiguitätsprinzip. Es besagt, dass zusammengehörige Informationen in räumlicher Nähe zueinander dargestellt werden sollten. Bei bildlichen Darstellungen sollten Erklärungen direkt integriert sein, also beispielsweise bei einem Diagramm die Legende nicht neben dem Diagramm dargestellt werden. Das Kontiguitätsprinzip gilt übrigens auch für zeitliche Zusammenhänge: in Erklärvideos sollten sich mündliche Erklärungen darauf beziehen, was in diesem Moment zu sehen ist.
Im folgenden Video wird Spanisch gesprochen. Auch ohne entsprechende Sprachkenntnisse können Sie vermutlich das Wesentliche bereits verstehen, wenn Sie auf die Zeichnung und Handbewegungen achten. Welchen Mehrwert könnte für (spanischsprachige) Schülerinnen und Schüler die mündliche Erklärung durch den Schüler gegenüber einer rein bildlichen Darstellung der Rechnung haben?
Lösung
Der Schüler erklärt jeden seiner Rechenschritte während er schreibt, zeichnet oder deutet: Die mündlich dargebotenen Informationen können die bildlich dargebotenen Informationen unterstützen, weil sie zeitlich passend zueinander dargeboten werden.
Potenziale digitaler Medien
Digitale Medien bieten noch weitere Möglichkeiten, bei der Entwicklung eines angemessenen Bruchzahlbegriffs zu unterstützen. Die meisten für die schulische Praxis verfügbaren digitalen Lernumgebungen (auch kommerzielle) sind hier allerdings noch stark eingeschränkt. In Forschungsprojekten werden dahingehend laufend neue Materialien entwickelt, die diese Möglichkeiten ausschöpfen. Zum Teil sind diese auch für die Nutzung im eigenen Unterricht geeignet, wie das im Projekt ALICE:Bruchrechnen entstandene digitale Schulbuch.
Unterstützung von Gesten
Innerhalb der Embodied Cognition-Theorie (en.: embodied cognition theory; Wilson, 2002) wird davon ausgegangen, dass Menschen dazu in der Lage sind, kognitive Belastung in Form von passenden Gesten oder Fingerbewegungen abzuladen. Ein Beispiel hierfür ist das Zählen mit den eigenen Fingern. Weiter wird angenommen, dass solche Handlungen losgelöst von ihren ursprünglichen sensomotorischen Zwecken auch rein kognitive Prozesse unterstützen können. Beispielsweise kann beim Erwerb des Bruchzahlbegriffs das konkrete Zerschneiden einer halben Pizza in zwei gleich große Stücke die Ausbildung einer Vorstellung des Erweiterns als Verfeinern einer Einteilung unterstützen. Auf Tablets und andere Touchscreens folgt die Blickbewegung beim Zerschneiden der Hand des Nutzers. Im Gegensatz dazu würde auf einem PC der Blick des Nutzers der Pizza auf dem Bildschirm – nicht der Maus auf dem Mousepad – folgen. Auch die Gesten zum Zerschneiden wären nicht mehr natürlich.
Adaptivität
Aufgaben können in digitalen Lernumgebungen derart implementiert werden, dass sie sich selbstständig an individuell unterschiedliche Lernprozesse einzelner Schülerinnen und Schüler anpassen (Leutner, 1993). Derartige adaptive Aufgabenformate können einen geeigneten Umgang mit Heterogenität innerhalb einer Klasse ermöglichen. So können Schülerinnen und Schüler unterschiedlicher Leistungsniveaus gleichermaßen gefördert werden. Lernumgebungen dieser Art werden als adaptiv bezeichnet, wenn die Eingaben von Schülerinnen und Schülern während des Arbeitens automatisiert zu Veränderungen der Parameter dieser Lernumgebung führt.
Feedback
Neben einer Anpassung des Schwierigkeitsgrades können digitale Lernumgebungen auch derart gestaltet sein, dass Schülerinnen und Schüler automatisch und umgehend eine auf ihre Antworten bezogene Rückmeldung (en.: Feedback) erhalten. Feedback kann auf die Lösung einer Aufgabe fokussieren (en.: corrective feedback), um auf konkrete Fehlvorstellungen aufmerksam zu machen sowie Rückmeldung über korrekte Antworten zu geben (Hattie & Timperley, 2007). Feedback kann sich aber auch auf den Prozess der Bearbeitung einer Aufgabe beziehen (en.: explanatory feedback) und Schülerinnen und Schüler dabei unterstützen, vorhandene Vorwissenslücken zu schließen, Fehlvorstellungen zu korrigieren und tiefgehendes Verständnis zu entwickeln (Hattie & Timperley, 2007).
Öffnen Sie das digitale Schulbuch auf Seite 23. Probieren Sie aus, die Pizzen zu zerschneiden und zu verschieben.
Öffnen Sie das digitale Schulbuch auf Seite 14. Die interaktive Aufgabe 13 erhöht den Schwierigkeitsgrad ein einziges Mal. Experimentieren Sie selbst mit der Aufgabe: Wann wird der Schwierigkeitsgrad erhöht? Wie äußert sich der Anstieg der Schwierigkeit? Wie reagiert die interaktive Aufgabe auf falsche Antworten? Welche Art von Feedback wird gegeben? Korrigierendes Feedback reicht für leistungsstärkere Schülerinnen und Schüler in der Regel aus. Erklärendes Feedback kann leistungsschwächere und leistungsstärkere Schülerinnen und Schüler besser unterstützen.
Probieren Sie auch Aufgabe 9 (S. 13 im iBook) und Aufgabe 86 (S. 65 im iBook) aus.
Materialien
Im Projekt ALICE:Bruchrechnen wurde ein interaktives und adaptives digitales Schulbuch für Tablet-PCs entwickelt. Es kann Schülerinnen und Schülern der sechsten Jahrgangsstufe mit unterschiedlichen Leistungsniveaus dabei unterstützen, eine tragfähige Vorstellung des Bruchzahlbegriffs zu entwickeln. Die Verwendung des eBook wird in einem Unterrichtsentwurf illustriert, der auf Seite 20 der Publikation beschrieben wird. Das Schulbuch ist kostenlos erhältlich und kompatibel mit iOS Geräten. Eine plattformunabhängige HTML-Version ist ebenfalls verfügbar.
Das digitale Schulbuch ist auch in einer kostenlosen Papierversion erhältlich. Es fehlen die interaktiven und adaptiven Funktionen. Sie können damit aber auch ohne digitale Endgeräte die forschungsbasierte Einführung in das Bruchrechnen nutzen.
Materialien aus einem Workshop für Lehrkräfte zum Thema “Einsatz digitaler Medien im Mathematik-Unterricht” umfassen Arbeitsblätter zu den Themen
- Anwendung von forschungsbasierten Konzepten wie der Cognitive Load Theorie auf Unterrichtsmaterialien und -entwürfe (Kapitel I)
- Einsatz von GeoGebra beim Ableiten (Kapitel II)
- Fachdidaktische Herausforderungen bei der Bruchrechnung (Kapitel III)
Adaptivität des digitalen Schulbuchs
Das eBook baut auf mathematikdidaktische und lernpsychologische Erkenntnisse auf. Es umfasst 90 Aufgaben, deren Reihenfolge an den Lernenden angepasst werden. So reagiert das Schulbuch während des Arbeitens flexibel auf eine Änderung der Schülerleistung, in dem leichtere oder schwierigere Aufgaben angeboten werden. Dafür wurden die Schwierigkeitsgrade der Aufgaben vorab auf Grundlage mathematikdidaktischer Erkenntnisse definiert. Das Schulbuch gibt zudem differenziertes Feedback zur Bearbeitung der Aufgabe. Hier werden zum Beispiel erklärende Rückmeldungen zu falschen Schülerantworten gegeben, die eine notwendige Überarbeitung bestehender Fehlkonzepte unterstützen sollen. Weitere Details werden auf Seite 13 der Publikation beschrieben.
Lernwirksamkeit des digitalen Schulbuchs
Im Forschungsprojekt ALICE:Bruchrechnen wurde die Lernwirksamkeit des digitalen Schulbuchs untersucht. Dazu wurde es in Gymnasien und Mittelschulen in Bayern eingesetzt. Welche Erfahrungen die Lehrkräfte dabei gemacht haben, ist in Kapitel 3 der Publikation beschrieben. Die Evaluation zeigte, dass insbesondere leistungsschwächere Schülerinnen und Schüler von der Verwendung des digitalen Schulbuchs profitieren. Die Möglichkeiten einer adaptiven Anpassung der Aufgabenschwierigkeit, individueller erklärender Rückmeldung unmittelbar nach der Bearbeitung von Aufgaben, interaktive Gestaltung anschaulicher Darstellungen sowie der Rückgriff auf passende Gesten bei der Interaktion mit der Lernumgebung zeigten sich bei Mittelschülerinnen und Mittelschülern als ausschlaggebende Faktoren für eine bessere Leistungsentwicklung im Bereich der Bruchrechnung. Leistungsstarke Schülerinnen und Schüler hingegen profitieren auch schon von einer analogen Variante des forschungsbasierten Schulbuchs, im Vergleich zu traditionellen Schulbüchern.
Für eilige Leser
Entwicklung des Bruchzahlbegriffs
Schülerinnen und Schüler haben erhebliche Probleme bei der Entwicklung einer tragfähigen Vorstellung von Bruchzahlen, wenn sie an Konzepten natürlicher Zahlen festhalten. Denn es gibt grundlegende Unterschiede bezüglich Darstellungen, Dichte, Größe und Operationen. Diese Unterschiede zu erkennen und zu verstehen ist notwendig, um einen angemessenen Bruchzahlbegriff zu entwickeln.
Gestaltung von Lernmaterialien
Das Interpretieren bildhafter Darstellungen und der Wechsel zwischen verschiedenen Darstellungsformen wie Pizzen und Schokoladentafeln fällt Schülerinnen und Schülern oft schwer. Die Anzahl von Informationen, die Lernende gleichzeitig verarbeiten können, ist beschränkt und hängt zum Beispiel von ihrem Vorwissen ab. Für das Lernen irrelevante Belastung sollte daher vermieden werden. Das Kontiguitätsprinzip besagt, dass zusammengehörige Informationen auch räumlich und/oder zeitlich zusammen präsentiert werden sollten. Zm Beispiel sollten in Erklärvideos mündliche Erklärungen sich darauf beziehen, was just in diesem Moment zu sehen ist.
Potenziale digitaler Medien
Digitale Medien bieten noch weitere Möglichkeiten, bei der Entwicklung eines angemessenen Bruchzahlbegriffs zu unterstützen. Sie können die Verwendung passender Gesten erlauben, die Lernumgebung an die Schülerinnen und Schülern anpassen und Feedback zu Lösungen geben. Die meisten für die schulische Praxis verfügbaren digitalen Lernumgebungen (auch kommerzielle) sind hier allerdings noch stark eingeschränkt. In Forschungsprojekten werden dahingehend laufend neue Materialien entwickelt, die diese Möglichkeiten ausschöpfen. Zum Teil sind diese auch für die Nutzung im eigenen Unterricht geeignet, wie das im Projekt ALICE:Bruchrechnen entstandene digitale Schulbuch.
Anregungen zur Umsetzung in der eigenen Praxis
- Wie kann ich das digitale Schulbuch in meinem Unterricht erproben?
- Wie kann ich die Theorie der kognitiven Belastung bei der Gestaltung meiner Arbeitsblätter berücksichtigen?
- Wie kann ich die Fortbildungsmaterialien in meiner nächsten Weiterbildung nutzen?
Weiterführende Quellen
Die Inhalte dieser Seite entstammen dem Projekt ALICE:Bruchrechnen der TU München. Vertiefende Informationen finden Sie in der Publikation “Tablet-PCs im Mathematikunterricht der Klasse 6. Ergebnisse des Forschungsprojektes ALICE:Bruchrechnen” von Frank Reinhold, Stefan Hoch, Bernhard Werner, Kristina Reiss und Jürgen Richter-Gebert. Sie können sie hier kostenlos herunterladen.
Evaluation
Die Evaluation des digitalen Schulbuchs wurde in der Fachzeitschrift Learning & Instruction publiziert:
Reinhold, F., Hoch, S., Werner, B., Richter-Gebert, J. & Reiss, K. (2020). Learning Fractions with and without Educational Technology: What Matters for High-Achieving and Low-Achieving Students? Learning and Instruction, 65, 101264. https://doi.org/10.1016/j.learninstruc.2019.101264
Zitierte Literatur
(1) Sweller, J., Ayres, P. & Kalyuga, S. (2011). Cognitive load theory. New York: Springer. doi:10.1007/978-1-4419-8126-4
(2) Mayer, R. E. (2014). Cognitive Theory of Multimedia Learning. In R. E. Mayer (Hrsg.), The Cambridge handbook of multimedia learning (2. Aufl., S. 31–48). New York: Cambridge University Press. doi:10.1017/CBO9781139547369.005